Technical Implementation
Cryptographic foundation of Silent Compliance VM - Use of DKG
Distributed Key Generation
Distributed Key Generation (DKG) is a critical tool for threshold cryptosystems. It allows a group of participants to collaboratively generate a shared public key and individual private key shares without any participant learning the others’ private keys. This process occurs without any intermediary (dealer). While the public key is generated openly, the private key remains confidential, known only through the shares held by participants. The secret key is used for cryptographic tasks such as signing or decryption, yet it is never computed or stored directly in the cryptosystem.
In a group of n participants, each holds a share of the secret key, and a subset of at least t participants is required to reconstruct the full secret for any cryptographic operation. This is known as a (t, n)-threshold scheme.
Shamir's Scheme
Shamir’s (t,n) — threshold scheme for sharing a secret s ∈ ℤₚ is defined as follows:
Distribution The dealer pics a random polynomial a(X) ∈ᵣ ℤₚ[X] of degree at most t satisfying a(0) = s. It sends share sᵢ = a(i) to participants Pᵢ, for i= 1,…,m.
Reconstruction Any set Q of t+1 participants may recover secret s from their shares by Lagrange interpolation:

Despite its elegance, this solution is insufficient for our use case. A malicious dealer can:
Send random values to some or all participants.
Use different polynomials while evaluating the shares.
Feldman's Enhancement
Feldman addresses these limitations in Shamir’s scheme by developing a verifiable secret sharing method, as detailed in Feldman’s Verifiable Secret Sharing. This ensures that participants can independently verify the validity of their received shares and confirm that the verification passes for all honest participants. Specifically, the dealer commits to the polynomial a(x) by broadcasting commitments Aᵢ = aᵢG for 0 < i < t. Participants can then confirm the validity of their shares comparing sᵢG against the calculates sum ∑ᵗⱼ=0 iʲAⱼ. If a participant receives an invalid share, they can raise a complaint.
While Feldman’s method ensures verifiable shares, it still relies on a dealer, introducing risks. If the dealer is malicious, they can distribute incorrect shares, undermining the system’s security. To mitigate this, we adopt the Joint-Feldman protocol, as described in Joint-Feldman DKG. This setup allows each participant to act as a dealer, contributing their own secret share. The final share for each participant is the sum of all shares they receive, ensuring no single party can manipulate the process. However, the participant responsible for an incorrect share must then provide the correct share or face disqualification from the process.
Non-Interactive Enhancement
We enhance this process by adopting a non-interactive approach using zero-knowledge proofs and smart contracts. Participants generate zero-knowledge proofs for their shares, attesting to the correctness of their computations, including the encryption of shares. These proofs, along with the shares and commitments, are submitted to a smart contract. The smart contract verifies the proofs and, upon successful validation, stores the shares and commitments. This setup significantly reduces the administrative burden on participants by eliminating the need for manual share verification. By leveraging zero-knowledge proofs, the protocol ensures computational integrity without revealing underlying data, thereby preserving privacy and security.
Description
Setup
The owner deploys the compliance contract on the Ghost Layer. Participants create a (Bob/jubjub) key pair, with the secret key z ∈ Fq and the public key X = xG, where G is the generator of G₁ curve and the q is (order/8, suborder).
Registration
The owner calls the register function in the compliance contract to register a public key and associate it with an index in Fq.
Secret Sharing
The participant:
Gets the index indᵢ associated with their public key from compliance contract.
Checks the index indᵢ is in Fq.
Generates a random polynomial a(X) ∈R ℤₚ[X] of degree at most t satisfying a(0) = x.
Computes the commitment values Aᵢ = aᵢG.
Computes the secret shares by evaluating the polynomial at the participants’ indices, sᵢ = a(indᵢ).
Generates a random scalar r to be used for encrypting the secret shares for the participants.
Encrypts the secret share sᵢ for participant i with public key Xᵢ using hashed ElGamal encryption: C₁ = rG, c₂ᵢ= s_i + Hₚ(rXᵢ) for all participants.
Computes the aggregated signs for C₁, Aᵢ’s and Xᵢ’s.
Prepares the public input yXᵢ’s, yC₁, c₂’s, Aᵢ’s, signs, indᵢ’s to the secret sharing circuit.
Stores the private input to the secret sharing circuit aᵢ’s, r
Creates the zero knowledge proof πᵢ attesting to

12. Calls shareSecret function with

and πᵢ.
shareSecret function
Checks all public keys are registered.
Checks the sender has shared their secret already.
Calls verification with inputs πᵢ, ssiᵢ, and indexes indˢⱼ₀, where indⱼ is the index bound with Xⱼ.
Stores commitment values.
Updates the compliance public key CPK by adding the sender’s public key to current CPK.
Member Gets Their Share
A successful call to the shareSecret function emits a SecretSharing event, including:
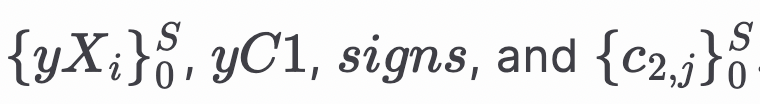
So, a member with the public key Xᵢ,
Finds the index of Xᵢ in the list of public keys yXˢᵢ₀, say i.
Unpacks C₁ using yC1 and signs.
Decrypts C₁, c₂ᵢ using xᵢ and gets the share by computing c₂ᵢ — H(xᵢC₁).
How Decryption Works
To de-anonymize the transactions, cP is needed, where c is the secret key corresponding to the compliance public key C and P is a point. So, participant Xᵢ
Decrypts all secret shares ssᵢⱼⁿⱼ₀ that are originated from the participants Xⱼ₀ⁿ contributed to the Compliance public key C=∑ⱼ₀ⁿ Xⱼ.
Computes ssᵢ = ∑ⱼ₀ⁿ ssᵢⱼ.
Finally, returns Dᵢ = ssᵢP as their decryption share.
When there are enough shares, the DAO:
Gets the indexes indⱼ₀ᵗ corresponding to Xⱼ’s.
Computes Lagrange coefficients:

3. Returns cP as:

Point Formats
To reduce input size and save gas, the contracts use a packed format to represent points. The circuit side natively supports 256 bits, but the coordinates of points on the BabyJubJub curve are 253 bits each, and an additional sign bit is required. This means a point’s coordinates and sign do not fit into a single 256-bit variable. Instead of sending a sign bit per point, we aggregate all signs into a single value. This allows us to switch between formats depending on the component we interact with, optimizing for efficiency.
Non-Native Arithmetic
For efficient scalar multiplications, we wanted to use a curve that its base field matches the native circuit field, hence BabyJubJub. However, polynomial operations need to be conducted in the scalar field of the curve, which necessitates non-native arithmetic modulo the curve order 𝑝. To achieve this, polynomial coefficients and evaluation points are represented as bigints, structured as fixed-size arrays of signals. Specifically, each bigint is divided into 4 limbs, with each limb being 64 bits. Thus, a polynomial coefficient aᵢ is expressed as

References
Sha79 Adi Shamir, “How to Share a Secret,” Communications of the ACM, vol. 22, no. 11, pp. 612–613, 1979, ACM New York, NY, USA.
Fel87 Paul Feldman, “A Practical Scheme for Non-Interactive Verifiable Secret Sharing,” in 28th Annual Symposium on Foundations of Computer Science (sfcs 1987), pp. 427–438, 1987, IEEE.
Last updated